


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Индексы (в статистике)
Определение "Индексы (в статистике)" в Большой Советской Энциклопедии
Индексы в статистике, относительные величины, количественно характеризующие сводную динамику (реже — изменение в пространстве) разносоставной совокупности. Так,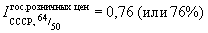
означает, что общий уровень всех розничных цен в государственной торговле СССР в 1964 по сравнению с уровнем их в 1950 был 0,76, или 76% (иначе говоря: взятые в совокупности, эти цены понизились с 1950 по 1964 в среднем на 0,24, или на 24% ). Совокупность является разносоставной по данному признаку, если итоговую величину этого признака во всей совокупности прямым, непосредственным суммированием его значений у отдельных единиц вычислить нельзя (например, натуральная величина продукции, состоящей из вещественно разных физических единиц или частей) или если такое суммирование, формально хотя и возможное, приводит к результату, лишённому экономического смысла (например, сумма цен вещественно разных товаров, взятых лишь по одной единице натурального измерения). Четырьмя элементами любого Индексы (в статистике) являются: а) индексируемая величина; б) тип (форма) Индексы (в статистике); в) веса Индексы (в статистике); г) сроки исчисления. В зависимости от элемента (а) возможны Индексы (в статистике) цен, Индексы (в статистике) физического (натурального) объёма продукции, Индексы (в статистике) производительности труда и т. д. В зависимости от типа (б) различают Индексы (в статистике) агрегатные и Индексы (в статистике) средние, а среди последних, смотря по форме средней, Индексы (в статистике) средние арифметические, Индексы (в статистике) средние геометрические, Индексы (в статистике) средние гармонические и т. д. В зависимости от весов (в) различают Индексы (в статистике) простые (невзвешенные) и Индексы (в статистике) взвешенные, а среди последних — Индексы (в статистике) с постоянными (неизменными) весами и Индексы (в статистике) с переменными весами (в меру необходимости с течением времени пересматриваемыми). В зависимости от сроков исчисления (г) рассматривают Индексы (в статистике) базисные (с постоянной, неизменной во времени базой) и Индексы (в статистике) цепные (если числовые значения индексируемой величины в каждый данный «текущий» срок сопоставляются с их значениями в предшествующий срок; иначе, Индексы (в статистике) с переменной базой); в общем случае произведение соответствующих цепных Индексы (в статистике) должно давать базисный Индексы (в статистике), например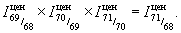
Индексы (в статистике) могут быть вычисляемы не только для всей разносоставной совокупности (общие, «тотальные» Индексы (в статистике)), но и для любой характерной части её, для любой существенной группы единиц (групповые Индексы (в статистике), или субиндексы), например: общий Индексы (в статистике) оптовых цен всех вообще товаров и групповые Индексы (в статистике) цен товаров продовольственных и цен товаров непродовольственных, или промышленных и сельскохозяйственных, или Индексы (в статистике) цен текстильных товаров, цен кожевенных товаров и т. д. Обычная относительная величина признака у какого-либо одного товара (например, относительное изменение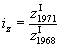
себестоимости z товара I за указанное трёхлетие) не есть Индексы (в статистике), хотя на практике обычно именуется, по аналогии, «индивидуальным Индексы (в статистике)» (себестоимости).
Труднейший вопрос при построении Индексы (в статистике) — выбор его весов и возможно более точное исчисление веса каждой группы, иногда и каждой единицы, входящей в индексируемую совокупность. Система таких весов должна отображать модель структуры того социально-экономического явления, динамика которого находит числовое выражение в Индексы (в статистике) Так, веса Индексы (в статистике) цен должны отражать товарную структуру торгового оборота (розничного, оптового), весами бюджетного индекса должны быть натуральные количества товаров и услуг, входящих в бюджетный набор, и т. п. В Индексы (в статистике) физического (натурального) объёма роль весов для натуральных количеств товаров играют неизменные цены, благодаря которым становится возможным «соизмерить» и свести воедино все части разносоставной натуральной совокупности; отсюда — частая общая, однако неправомерная, трактовка любых весов Индексы (в статистике) как «коэффициентов соизмерения», «коэффициентов сведения» частей разносоставной совокупности.
К рудиментарным прообразам Индексы (в статистике) прибегали уже два столетия (и даже более) тому назад. Так, в 1738 Дюто (Франция) сопоставил суммы цен набора из единиц некоторых товаров и опубликовал их отношение  в 1764 Дж. Карли (Италия) вычислил примитивный невзвешенный арифметический Индексы (в статистике) изменения цен трёх товаров (хлеб, вино, оливковое масло) за четверть тысячелетия (с 1500 по 1750); в 1798, независимо от Карли, Дж. Шакберг (Великобритания) стал вычислять таким же способом
в 1764 Дж. Карли (Италия) вычислил примитивный невзвешенный арифметический Индексы (в статистике) изменения цен трёх товаров (хлеб, вино, оливковое масло) за четверть тысячелетия (с 1500 по 1750); в 1798, независимо от Карли, Дж. Шакберг (Великобритания) стал вычислять таким же способом 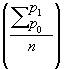 Индексы (в статистике) оптовых цен десятка товаров, а в 1812 А. Янг (Великобритания) ввёл в этот Индексы (в статистике) веса (от 1 до 5 для разных товаров). Однако лишь спустя полстолетия (вследствие обесценения серебра и вызванного этим общего роста мировых цен, особенно в 60-х гг.) в Великобритании начались систематическое исчисление и публикация Индексы (в статистике) оптовых цен. Главные из них: Индексы (в статистике) журнала «Economist» (с 1869, по формуле
Индексы (в статистике) оптовых цен десятка товаров, а в 1812 А. Янг (Великобритания) ввёл в этот Индексы (в статистике) веса (от 1 до 5 для разных товаров). Однако лишь спустя полстолетия (вследствие обесценения серебра и вызванного этим общего роста мировых цен, особенно в 60-х гг.) в Великобритании начались систематическое исчисление и публикация Индексы (в статистике) оптовых цен. Главные из них: Индексы (в статистике) журнала «Economist» (с 1869, по формуле 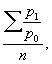 для 22 товаров; с 1920 — уже для 44 товаров; это старейший из существующих ныне Индексы (в статистике)) и Индексы (в статистике) Зауэрбека (с 1886), а затем, как его продолжение, Индексы (в статистике) журнала «Statist» (для 36 товаров, по той же формуле). В США Индексы (в статистике) цен был впервые исчислен Н. Бурхардтом в 1881 (за 1824—80). Основы современной теории Индексы (в статистике) цен были заложены трудами У. Джевонса (Великобритания, 1863 и 1865), Э. Ласпейреса (1871) и Г. Пааше (Германия, 1874). В России первые Индексы (в статистике) оптовых цен публиковались в серии ежегодников «Свод товарных цен» (за 1890—1915, для 45 товаров, по формуле невзвешенной арифметической средней). Первая мировая война 1914—18 повлекла за собой огромные сдвиги цен на мировом рынке и в народном хозяйстве отдельных государств; для их изучения и измерения потребовались многие новые, до того неизвестные, Индексы (в статистике) розничных цен, Индексы (в статистике) «стоимости жизни» впервые в Великобритании, 1918, и в США, 1919) Индексы (в статистике) физического объёма экономических явлений (элиминировавшие фактор непрерывно меняющихся цен), Индексы (в статистике) покупательной силы валютных единиц (в связи с крушением мировой системы золотого монометаллизма и попытками заменить валютные курсы «паритетами покупательной силы» валют), различные Индексы (в статистике) для изучения конъюнктуры и др. Поэтому последнее полустолетие (с 1918) стало новым этапом истории Индексы (в статистике), отмеченным небывалым развитием индексного метода статистической науки и расширением практики Индексы (в статистике) В СССР уже с 1918 началось исчисление прожиточного минимума рабочих, перешедшее в 1922 в исчисление бюджетного индекса; в 1919—21 — исчисление и публикация индексов Конъюнктурного института; с августа 1922 — публикация И оптовых цен Госплана. В планово развивающемся народном хозяйстве СССР (а после второй мировой войны 1939—45 и других социалистических государств) потребовалось построение и регулярное исчисление множества новых Индексы (в статистике), особенно Индексы (в статистике) плановых заданий и Индексы (в статистике) степени выполнения плана. 20-е гг., а затем десятилетие 1956—65 были годами, особенно интенсивного развития теории советского индексного метода как одного из мощных познавательных средств современной советской статистики.
для 22 товаров; с 1920 — уже для 44 товаров; это старейший из существующих ныне Индексы (в статистике)) и Индексы (в статистике) Зауэрбека (с 1886), а затем, как его продолжение, Индексы (в статистике) журнала «Statist» (для 36 товаров, по той же формуле). В США Индексы (в статистике) цен был впервые исчислен Н. Бурхардтом в 1881 (за 1824—80). Основы современной теории Индексы (в статистике) цен были заложены трудами У. Джевонса (Великобритания, 1863 и 1865), Э. Ласпейреса (1871) и Г. Пааше (Германия, 1874). В России первые Индексы (в статистике) оптовых цен публиковались в серии ежегодников «Свод товарных цен» (за 1890—1915, для 45 товаров, по формуле невзвешенной арифметической средней). Первая мировая война 1914—18 повлекла за собой огромные сдвиги цен на мировом рынке и в народном хозяйстве отдельных государств; для их изучения и измерения потребовались многие новые, до того неизвестные, Индексы (в статистике) розничных цен, Индексы (в статистике) «стоимости жизни» впервые в Великобритании, 1918, и в США, 1919) Индексы (в статистике) физического объёма экономических явлений (элиминировавшие фактор непрерывно меняющихся цен), Индексы (в статистике) покупательной силы валютных единиц (в связи с крушением мировой системы золотого монометаллизма и попытками заменить валютные курсы «паритетами покупательной силы» валют), различные Индексы (в статистике) для изучения конъюнктуры и др. Поэтому последнее полустолетие (с 1918) стало новым этапом истории Индексы (в статистике), отмеченным небывалым развитием индексного метода статистической науки и расширением практики Индексы (в статистике) В СССР уже с 1918 началось исчисление прожиточного минимума рабочих, перешедшее в 1922 в исчисление бюджетного индекса; в 1919—21 — исчисление и публикация индексов Конъюнктурного института; с августа 1922 — публикация И оптовых цен Госплана. В планово развивающемся народном хозяйстве СССР (а после второй мировой войны 1939—45 и других социалистических государств) потребовалось построение и регулярное исчисление множества новых Индексы (в статистике), особенно Индексы (в статистике) плановых заданий и Индексы (в статистике) степени выполнения плана. 20-е гг., а затем десятилетие 1956—65 были годами, особенно интенсивного развития теории советского индексного метода как одного из мощных познавательных средств современной советской статистики.
Лит.: Немчинов В. С., Сельскохозяйственная статистика с основами общей теории, Избр. произв., т. 2, М., 1967, гл. 19; Суслов Индексы (в статистике) П., Общая теория статистики, М., 1970; Статистический словарь, М., 1965 [статьи об индексах]; «Уч. зап. по статистике АН СССР», 1955, т. 1; 1959, т. 5; 1963, т. 7; Югенбург С. М., Индексный метод в советской статистике, М., 1958; Перегудов В. Н., Теоретические вопросы индексного анализа, М., 1960; Казинец Л. С., Теория индексов (Основные вопросы), М., 1963; Яновский А. С., Русские индексы, в кн.: Фишер Индексы (в статистике), Построение индексов, [пер. с англ.], М., 1928 (приложение 6, с. 391—438); Фишер Индексы (в статистике), Этапы истории индексов, там же (приложение 4, с. 378—81); Четвериков Н. С., Статистические и стохастические исследования, М., 1963, с. 13—56.
Ф. Д. Лившиц.
| "БСЭ" >> "И" >> "ИН" >> "ИНД" >> "ИНДЕ" |
Статья про "Индексы (в статистике)" в Большой Советской Энциклопедии была прочитана 486 раз
| Бургер двойного помола |
| Английский рыбный пирог |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс