


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Квантовые числа
Определение "Квантовые числа" в Большой Советской Энциклопедии
Квантовые числа, целые (0, 1, 2,...) или полуцелые (1/2, 3/2, 5/2,...) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы. Применение Квантовые числа в квантовой механике отражает черты дискретности процессов, протекающих в микромире, и тесно связано с существованием кванта действия, или Планка постоянной, 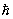 . Квантовые числа были впервые введены в физику для описания найденных эмпирически закономерностей атомных спектров (см. Атом), однако смысл Квантовые числа и связанной с ними дискретности некоторых величин, характеризующих динамику микрочастиц, был раскрыт лишь квантовой механикой.
. Квантовые числа были впервые введены в физику для описания найденных эмпирически закономерностей атомных спектров (см. Атом), однако смысл Квантовые числа и связанной с ними дискретности некоторых величин, характеризующих динамику микрочастиц, был раскрыт лишь квантовой механикой.
Набор Квантовые числа, исчерпывающе определяющий состояние квантовой системы, называется полным. Совокупность состояний, отвечающих всем возможным значениям Квантовые числа из полного набора, образует полную систему состояний. Состояние электрона в атоме определяется четырьмя Квантовые числа соответственно четырём степеням свободы электрона (3 степени свободы связаны с тремя координатами, определяющими пространственное положение электрона, а четвёртая, внутренняя, степень свободы - с его спином). Для атома водорода и водородоподобных атомов эти Квантовые числа, образующие полный набор, следующие.
Главное Квантовые числа n = 1, 2, 3,... определяет уровни энергии электрона.
Азимутальное (или орбитальное) Квантовые числа l = 0, 1, 2,..., n -1 задаёт спектр возможных значений квадрата орбитального момента количества движения электрона: 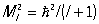 .
.
Магнитное Квантовые числа ml характеризует возможные значения проекции Mlz орбитального момента Ml на некоторое, произвольно выбранное, направление (принимаемое за ось z):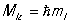 ; может принимать целые значения в интервале от - l до + l (всего 2 l + 1 значений).
; может принимать целые значения в интервале от - l до + l (всего 2 l + 1 значений).
Магнитное спиновое К, ч., или просто спиновое Квантовые числа, ms характеризует возможные значения проекции спина электрона и может принимать 2 значения:
ms = ± 1/2.
Задание состояния электрона с помощью Квантовые числа n, l, ml и ms не учитывает так называемой тонкой структуры энергетических уровней - расщепления уровней с данным n (при n ³ 2) в результате влияния спина на орбитальное движение электрона (см. Спин-орбитальное взаимодействие). При учёте этого взаимодействия для характеристики состояния электрона вместо ml и ms применяют Квантовые числа j и mj).
Квантовые числа j полного момента количества движениям электрона (орбитального плюс спинового) определяет возможные значения квадрата полного момента: 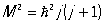 и при заданном l может принимать 2 значения: j = l ± 1/2.
и при заданном l может принимать 2 значения: j = l ± 1/2.
Магнитное квантовое число полного моментах; определяет возможные значения проекции полного момента на ось z, Mz = hmj; может принимать 2l + 1 значений: mj = -j, -j + 1,..., + j.
Те же Квантовые числа приближённо описывают состояния отдельных электронов в сложных (многоэлектронных) атомах (а также состояния отдельных нуклонов - протонов и нейтронов - в атомных ядрах). В этом случае n нумерует последовательные (в порядке возрастания энергии) уровни энергии с заданным l. Состояние же многоэлектронного атома в целом определяется следующими Квантовые числа: Квантовые числа полного орбитального момента атома L, определяемого движением всех электронов, L = 0, 1, 2,...; Квантовые числа полного момента атома J, которое может принимать значения с интервалом в 1 от J = |L-S| до J = |L + S|, где S - полный спин атома (в единицах 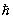 ); магнитным квантовым числом mj, определяющим возможные значения проекции полного момента атома на ось z,
); магнитным квантовым числом mj, определяющим возможные значения проекции полного момента атома на ось z, 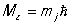 и принимающим 2J + 1 значений.
и принимающим 2J + 1 значений.
Для характеристики состояния атома и вообще квантовой системы вводят ещё одно Квантовые числа - чётность состояния Р, которое принимает значения + 1 или - 1 в зависимости от того, сохраняет волновая функция, определяющая состояние системы, знак при отражении координат r относительно начала координат (т. е. при замене r ® - r) или меняет его на обратный. Чётность Р для атома водорода равна (-1) l, а для многоэлектронных атомов (-1) L.
Квантовые числа оказались также удобными для формулировки отбора правил, определяющих возможные типы квантовых переходов.
В физике элементарных частиц и в ядерной физике вводится ряд др. Квантовые числа Квантовые числа элементарных частиц - это внутренние характеристики частиц, определяющие их взаимодействия и закономерности взаимных превращений. Кроме спина s, который может быть целым или полуцелым числом (в единицах 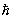 ), к ним относятся: электрический заряд Q - у всех известных элементарных частиц равен либо 0, либо целому числу, положительному или отрицательному (в единицах величины заряда электрона е); барионный заряд В - равен 0 или 1 (для античастиц 0, -1); лептонные заряды, или лептонные числа, - электронное Le и мюонное Lm, равны 0 или +1 (для античастиц 0, -1); изотопический спин Т - целое или полуцелое число; странность S или гиперзаряд Y (связанный с S соотношением Y = S + В) - все известные элементарные частицы (или античастицы) имеют S = 0 или ± 1, ± 2, ± 3; внутренняя чётность П - Квантовые числа, характеризующее свойства симметрии элементарных частиц относительно отражений координат, может быть равна + 1 (такие частицы называют чётными) и -1 (нечётные частицы), и некоторые др. Квантовые числа Эти Квантовые числа применяются и к системам из нескольких элементарных частиц, в том числе к атомным ядрам. При этом полные значения электрического, барионного и лептонного зарядов и странности системы частиц равны алгебраической сумме соответствующих Квантовые числа отдельных частиц, полный спин и изотопический спин получаются по квантовым правилам сложения моментов, а внутренние чётности частиц перемножаются.
), к ним относятся: электрический заряд Q - у всех известных элементарных частиц равен либо 0, либо целому числу, положительному или отрицательному (в единицах величины заряда электрона е); барионный заряд В - равен 0 или 1 (для античастиц 0, -1); лептонные заряды, или лептонные числа, - электронное Le и мюонное Lm, равны 0 или +1 (для античастиц 0, -1); изотопический спин Т - целое или полуцелое число; странность S или гиперзаряд Y (связанный с S соотношением Y = S + В) - все известные элементарные частицы (или античастицы) имеют S = 0 или ± 1, ± 2, ± 3; внутренняя чётность П - Квантовые числа, характеризующее свойства симметрии элементарных частиц относительно отражений координат, может быть равна + 1 (такие частицы называют чётными) и -1 (нечётные частицы), и некоторые др. Квантовые числа Эти Квантовые числа применяются и к системам из нескольких элементарных частиц, в том числе к атомным ядрам. При этом полные значения электрического, барионного и лептонного зарядов и странности системы частиц равны алгебраической сумме соответствующих Квантовые числа отдельных частиц, полный спин и изотопический спин получаются по квантовым правилам сложения моментов, а внутренние чётности частиц перемножаются.
В широком смысле Квантовые числа часто называют физические величины, определяющие движение квантовомеханической частицы (или системы), сохраняющиеся в процессе движения, но не обязательно принадлежащие к дискретному спектру возможных значений. Например, энергию свободно движущегося электрона (имеющую непрерывный спектр значений) можно рассматривать как одно из его Квантовые числа
Лит. см. при ст. Атомная физика, Элементарные частицы.
Д. В. Гальцов.
| "БСЭ" >> "К" >> "КВ" >> "КВА" >> "КВАН" |
Статья про "Квантовые числа" в Большой Советской Энциклопедии была прочитана 1325 раз
| Пицца в сковороде |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс