


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Комплексные числа
Определение "Комплексные числа" в Большой Советской Энциклопедии
 |
| Комплексные числа. Рис. |
r (cos j + i sin j)
(тригонометрическая, или полярная, форма Комплексные числа);
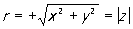 называют модулем Комплексные числа х+iy, а j = arg z — аргументом его. Тригонометрическая форма Комплексные числа особенно удобна для действий возведения в степень и извлечения корня:
называют модулем Комплексные числа х+iy, а j = arg z — аргументом его. Тригонометрическая форма Комплексные числа особенно удобна для действий возведения в степень и извлечения корня:
[r (cos j + i sin j)] n = rn (cos nj + i sin nj),
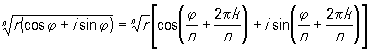 , в частности
, в частности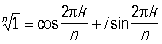 , k = 0, 1, …, n—1
, k = 0, 1, …, n—1
По своим алгебраическим свойствам совокупность Комплексные числа образует поле. Это поле алгебраически замкнуто, т. е. любое уравнение xn + a1xn-1+...+an =0; где a1,..., an — Комплексные числа, имеет (при учёте кратности) среди Комплексные числа точно n корней.
Уже в древности математики сталкивались в процессе решения некоторых задач с извлечением квадратного корня из отрицательных чисел; в этом случае задача считалась неразрешимой. Когда же в 1-й половине 16 в. были найдены формулы для решения кубических уравнений, оказалось, что в так называемом неприводимом случае действительные корни уравнений с действительными коэффициентами получаются в результате действий над Комплексные числа Это содействовало признанию Комплексные числа Первое обоснование простейших действий с Комплексные числа встречается у Р. Бомбелли в 1572. Однако долгое время к Комплексные числа относились, как к чему-то сверхъестественному. Так, Г. Лейбниц в 1702 писал: «Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием». В 1748 Л. Эйлер нашёл замечательную формулу eij = cosj + isinj, явившуюся первым важным результатом теории функций комплексного переменного, но истинный характер Комплексные числа выяснился лишь к концу 18 в., когда была открыта их геометрическая интерпретация (см. выше). Термин «Комплексные числа» предложен К. Гауссом в 1831. Введение Комплексные числа делает многие математические рассмотрения более единообразными и ясными и является важным этапом в развитии понятия о числе (см. Число). Комплексные числа Употребляются теперь при математическом описании многих вопросов физики и техники (в гидродинамике, аэромеханике, электротехнике, атомной физике и т.д.). Основные разделы классического математического анализа приобретают полную ясность и законченность только при использовании Комплексные числа, чем обусловливается центральное место, занимаемое теорией функций комплексного переменного. См. Аналитические функции.
Лит.: Маркушевич А. И., Комплексные числа и конформные отображения, 2 изд., М., 1960; Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968.
| "БСЭ" >> "К" >> "КО" >> "КОМ" >> "КОМП" |
Статья про "Комплексные числа" в Большой Советской Энциклопедии была прочитана 719 раз
| Бургер двойного помола |
| Яйца в кляре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс