Максвелла распределение

Определение "Максвелла распределение" в Большой Советской Энциклопедии

Максвелла распределение

Максвелла распределение, распределение по скоростям (или импульсам) молекул системы, находящейся в состоянии термодинамического равновесия. Впервые установлено Дж. К. Максвеллом в 1859. Согласно Максвелла распределение, вероятность Dw (v_x, v_y, v_z) того, что проекции скорости молекулы лежат в малых интервалах от v_x до v_x + Dv_x, от v_y до v_y + Dv_y и от v_z до v_z + Dv_z определяется формулой:
   (1)
Здесь m - масса молекулы, Т - абсолютная температура системы, k - постоянная Больцмана.
Вероятность того, что абсолютное значение скорости лежит в интервале от v до v + Dv, вытекает из (1) и имеет вид:
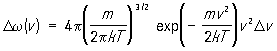   (2)
Эта вероятность достигает максимума при

Скорость v₀ называется наиболее вероятной. Чем ниже температура системы, тем большее число молекул имеют скорости, близкие к наиболее вероятной (см. рисунок).

Среднее число частиц в 1 см³ газа со скоростями в интервале от v до v + Dv равно Dn(v) = n₀ Dw(v), где n₀ - полное число частиц в 1 см³.

С помощью Максвелла распределение можно вычислять средние значения скоростей молекул и любых функций этих скоростей. В частности, средняя квадратичная скорость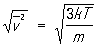  

лишь немного (в 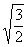 раз) превышает наиболее вероятную скорость. Например, для азота при Т » 300 К  м/сек, a v₀ » 360 м/сек.

Максвелла распределение вытекает из Гиббса распределения канонического в том случае, когда поступательное движение частиц можно рассматривать в классическом приближении (см. Статистическая физика). Максвелла распределение не зависит от характера взаимодействия частиц системы и от внешних сил и потому справедливо как для молекул газа, так и для молекул жидкостей и твёрдых тел. Максвелла распределение справедливо также для броуновских частиц, взвешенных в газе или жидкости (см. Броуновское движение).
Экспериментальное подтверждение Максвелла распределение получено в опытах с молекулярными пучками.
Лит.: Кикоин И. К., Кикоин А. К., Молекулярная физика, М., 1963; Штрауф Е. А., Молекулярная физика, Л. - М., 1949.
  Г. Я. Мякишев.