


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Натуральное исчисление
Определение "Натуральное исчисление" в Большой Советской Энциклопедии
Натуральное исчисление, исчисление естественного вывода, натуральная дедукция, общее название логических исчислений, введённых и изученных в 1934 немецким логиком Г. Генценом (и независимо польским логиком С. Яськовским) с целью формализации процесса логического вывода, как можно более точно воспроизводящей структуру обычных содержательных рассуждений, а также для решения ряда важных задач метаматематики (в том числе для доказательства непротиворечивости арифметики натуральных чисел). Основным объектом Натуральное исчисление можно считать отношение (формальной) выводимости, обозначаемое символом  , обладающее, по определению, свойством А
, обладающее, по определению, свойством А 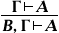 (разрешение усилить посылки),
(разрешение усилить посылки), 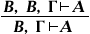 (разрешение опускать одну из совпадающих посылок),
(разрешение опускать одну из совпадающих посылок), 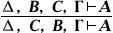
Введение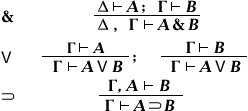
(так называемая «теорема о дедукции», см. Дедукция)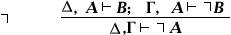
(reductio ad absurdum, или приведение к нелепости, см. Доказательство от противного) Удаление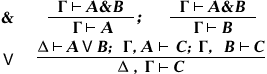
(так называемое доказательство разбором случаев)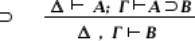
(modus ponens, или схема заключения)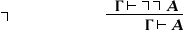
(так называемый закон снятия двойного отрицания). (В скобках указана интерпретация некоторых правил в терминах традиционной логики; интерпретация остальных правил — та же, что у соответствующих аксиом обычного исчисления высказываний, перефразировками которых они являются.) Добавление к этому списку соответствующих правил введения и удаления для кванторов приводит к Натуральное исчисление предикатов. Замена правила  -удаления на так называемое правило слабого
-удаления на так называемое правило слабого 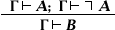 («из противоречия следует любое высказывание», см. Противоречия принцип) приводит к интуиционистскому (конструктивному) Натуральное исчисление высказываний (а с подходящими изменениями в кванторных правилах — к интуиционистскому Натуральное исчисление предикатов; см. Математический интуиционизм, Конструктивное направление).
(«из противоречия следует любое высказывание», см. Противоречия принцип) приводит к интуиционистскому (конструктивному) Натуральное исчисление высказываний (а с подходящими изменениями в кванторных правилах — к интуиционистскому Натуральное исчисление предикатов; см. Математический интуиционизм, Конструктивное направление).
Доказательство в Натуральное исчисление — это, как обычно, вывод из пустого множества посылок. В формулировках Натуральное исчисление, подобных приведённой, в которых нет аксиом (кроме, быть может, А А), источником получения «логических законов», выражаемых формулами, доказуемыми без привлечения каких бы то ни было гипотез (посылок), оказывается правило É-введения. Гибкость аппарата Натуральное исчисление, близость его к привычным формам содержательных рассуждений и простота получающихся выводов делают его удобным орудием логико-математического исследования. Натуральное исчисление полезно и в тех случаях, когда применяются другие системы логики: в качестве источника выводимых (дополнительных) правил вывода, применение которых также значительно упрощает логический аппарат, а также для получения эвристических (предварительных, подлежащих дальнейшему обоснованию) доводов, которые так или иначе должны предшествовать любому формальному доказательству (как источник доказываемых или опровергаемых гипотез).
Лит.: Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, §§ 20, 23; Генцен Г., Исследования логических выводов, пер. с. нем., в кн.: Математическая теория логического вывода, М., 1967; Карри Х. Б., Основания математической логики, пер. с англ., М., 1969. См. также лит. при ст. Правило вывода.
Ю. А. Гастов.
| "БСЭ" >> "Н" >> "НА" >> "НАТ" |
Статья про "Натуральное исчисление" в Большой Советской Энциклопедии была прочитана 604 раз
| Бургер двойного помола |
| Бургер двойного помола |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс