


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Нормаль
Определение "Нормаль" в Большой Советской Энциклопедии
Нормаль (франц. normal, от лат. normalis — прямой) к кривой (к поверхности) в данной её точке — прямая, проходящая через эту точку и перпендикулярная к касательной прямой (касательной плоскости) в этой же точке кривой (поверхности). Плоская кривая имеет в каждой точке единственную Нормаль, расположенную в плоскости кривой. Если х = f (t) и у = g (t) — параметрические уравнения плоской кривой L, то уравнение Нормаль в точке (x0, y0) кривой L, соответствующей значению t0 параметра t, может быть записано в виде: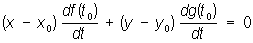 .
.
Для плоской кривой, заданной уравнением F (х, у) = 0, уравнение Нормаль имеет вид: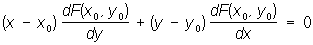 .
.
Пространственная кривая имеет в каждой своей точке бесчисленное множество Нормаль, заполняющих некоторую плоскость (нормальную плоскость). Нормаль, лежащая в соприкасающейся плоскости, называется главной нормалью. Нормаль, перпендикулярную к соприкасающейся плоскости, называется бинормалью. Касательная, главная Нормаль и бинормаль образуют подвижный триэдр кривой.
Для поверхности, заданной уравнением F (х, у, z) = 0, Нормаль может быть представлена уравнениями: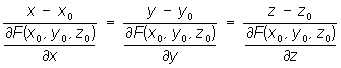 .
.
Понятие Нормаль играет существенную роль не только в дифференциальной геометрии, но и в различных её приложениях: в геометрической оптике (например, в формулировке основных законов преломления и отражения световых лучей), в механике (материальная точка или тело при перемещениях по гладким линиям или поверхностям испытывают реакцию, направленную по Нормаль, в консервативном поле силовые линии в каждой точке имеют направление Нормаль к изопотенциальной поверхности, проходящей через эту точку, и т.д.).
| "БСЭ" >> "Н" >> "НО" >> "НОР" >> "НОРМ" |
Статья про "Нормаль" в Большой Советской Энциклопедии была прочитана 553 раз
| Панайпай |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс