


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Общий интеграл
Определение "Общий интеграл" в Большой Советской Энциклопедии
Общий интеграл обыкновенного дифференциального уравнения
F (x, у, у",..., y (n)) =0
— соотношение
F(х, у, C1,..., Cn) =0,
содержащее и существенных произвольных постоянных C1,..., Cn, следствием которого является данное дифференциальное уравнение (см. Дифференциальные уравнения). Иными словами, это уравнение должно представлять собой результат исключения постоянных C1 (i = 1,..., n) из уравнений: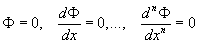 , (*)
, (*)
причём эти постоянные существенны в том смысле, что процесс исключения их из системы (*) не может привести к дифференциальному уравнению, отличному от данного. Общий интеграл тесно связан с общим решением. Если постоянным Ci, входящим в Общий интеграл, дать определённые значения, то получим частый интеграл. Неполное исключение постоянных Ci из системы (*) приводит к промежуточному интегралу
Fk (х, у, у",..., у (n-k)), C1,..., Ck = 0
(где 1 £ k £ n—1); в частности, при k = 1— к первому интегралу. Геометрически Общий интеграл представляет n-параметрическое семейство интегральных кривых.
Лит.: Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959.
| "БСЭ" >> "О" >> "ОБ" >> "ОБЩ" |
Статья про "Общий интеграл" в Большой Советской Энциклопедии была прочитана 493 раз
| Коптим скумбрию в коробке |
| Крабы в кокосовом молоке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс