


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Операторы
Определение "Операторы" в Большой Советской Энциклопедии
Операторы в квантовой теории, математическое понятие, широко используемое в математическом аппарате квантовой механики и квантовой теории поля и служащее для сопоставления определённому вектору состояния (или волновой функции) y др. определённых векторов (функций) y". Соотношение между y и y" записывается в виде y" = 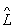 y, где
y, где 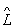 - оператор. В квантовой механике физическим величинам (координате, импульсу, моменту количества движения, энергии и т.д.) ставятся в соответствие Операторы
- оператор. В квантовой механике физическим величинам (координате, импульсу, моменту количества движения, энергии и т.д.) ставятся в соответствие Операторы  (Операторы координаты, Операторы импульса и т.д.), действующие на вектор состояния (или волновую функцию) y, т. е. на величину, описывающую состояние физической системы.
(Операторы координаты, Операторы импульса и т.д.), действующие на вектор состояния (или волновую функцию) y, т. е. на величину, описывающую состояние физической системы.
Простейшие виды Операторы, действующих на волновую функцию y(х) (где х - координата частицы), - Операторы умножения (например, Операторы координаты 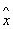 ,
,  y = хy) и о. дифференцирования (например, Операторы импульса
y = хy) и о. дифференцирования (например, Операторы импульса  ,
, 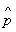 y =
y =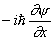 , где i - мнимая единица,
, где i - мнимая единица,  - постоянная Планка). Если y - вектор, компоненты которого можно представить в виде столбца чисел, то Операторы представляет собой квадратную таблицу - матрицу.
- постоянная Планка). Если y - вектор, компоненты которого можно представить в виде столбца чисел, то Операторы представляет собой квадратную таблицу - матрицу.
В квантовой механике в основном используются линейные операторы. Это означает, что они обладают следующим свойством: если  y1 = y"1 и
y1 = y"1 и 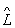 y2 = y"2, то
y2 = y"2, то 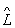 (c1y1 + c2y2) = c1y"1 + c2y"2, где c1 и с2 - комплексные числа. Это свойство отражает суперпозиции принцип - один из основных принципов квантовой механики.
(c1y1 + c2y2) = c1y"1 + c2y"2, где c1 и с2 - комплексные числа. Это свойство отражает суперпозиции принцип - один из основных принципов квантовой механики.
Существенные свойства Операторы 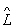 определяются уравнением
определяются уравнением 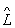 yn = lnyn, где ln - число. Решения этого уравнения yn называется собственными функциями (собственными векторами) оператора
yn = lnyn, где ln - число. Решения этого уравнения yn называется собственными функциями (собственными векторами) оператора  . Собственные волновые функции (собственные векторы состояния) описывают в квантовой механике такие состояния, в которых данная физическая величина L имеет определённое значение ln. Числа ln называется собственными значениями Операторы
. Собственные волновые функции (собственные векторы состояния) описывают в квантовой механике такие состояния, в которых данная физическая величина L имеет определённое значение ln. Числа ln называется собственными значениями Операторы 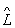 , а их совокупность - спектром Операторы Спектр может быть непрерывным или дискретным; в первом случае уравнение, определяющее y n, имеет решение при любом значении ln (в определённой области), во втором - решения существуют только при определённых дискретных значениях ln. Спектр Операторы может быть и смешанным: частично непрерывным, частично дискретным. Например, Операторы координаты и импульса имеют непрерывный спектр, а Операторы энергии в зависимости от характера действующих в системе сил - непрерывный, дискретный или смешанный спектр. Дискретные собственные значения Операторы энергии называются энергетическими уровнями.
, а их совокупность - спектром Операторы Спектр может быть непрерывным или дискретным; в первом случае уравнение, определяющее y n, имеет решение при любом значении ln (в определённой области), во втором - решения существуют только при определённых дискретных значениях ln. Спектр Операторы может быть и смешанным: частично непрерывным, частично дискретным. Например, Операторы координаты и импульса имеют непрерывный спектр, а Операторы энергии в зависимости от характера действующих в системе сил - непрерывный, дискретный или смешанный спектр. Дискретные собственные значения Операторы энергии называются энергетическими уровнями.
Собственные функции и собственные значения Операторы физических величин должны удовлетворять определённым требованиям. Т. к. непосредственно измеряемые физич. величины всегда принимают веществ. значения, то соответствующие квантовомеханич. Операторы должны иметь веществ. собств. значения. Далее, поскольку в результате измерения физич. величины в любом состоянии y должно получаться одно из возможных собств. значений этой величины, необходимо, чтобы произвольная волновая функция (вектор состояния) могла быть представлена в виде линейной комбинации собств. функций (векторов) yn Операторы этой физич. величины; др. словами, совокупность собств. функций (векторов) должна представлять полную систему. Этими свойствами обладают собств. функции и собств. значения т.н. самосопряжённых Операторы, или эрмитовых операторов.
С Операторы можно производить алгебраич. действия. В частности, под произведением Операторы  1 и
1 и  2 понимается такой Операторы
2 понимается такой Операторы  =
= 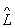 1
1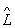 2, действие которого на вектор (функцию) y даёт
2, действие которого на вектор (функцию) y даёт  y = y’’, если
y = y’’, если 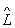 2y = y’ и
2y = y’ и 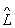 1y’ = y’’. Произведение Операторы в общем случае зависит от порядка сомножителей, т. е.
1y’ = y’’. Произведение Операторы в общем случае зависит от порядка сомножителей, т. е.  1
1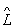 2 ¹
2 ¹ 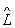 2
2 1. Этим алгебра Операторы отличается от обычной алгебры чисел. Возможность перестановки порядка сомножителей в произведении двух Операторы тесно связана с возможностью одновременного измерения физических величин, которым отвечают эти Операторы Необходимым и достаточным условием одновременной измеримости физических величин является равенство
1. Этим алгебра Операторы отличается от обычной алгебры чисел. Возможность перестановки порядка сомножителей в произведении двух Операторы тесно связана с возможностью одновременного измерения физических величин, которым отвечают эти Операторы Необходимым и достаточным условием одновременной измеримости физических величин является равенство  1
1 2 =
2 =  2
2 1 (см. Перестановочные соотношения).
1 (см. Перестановочные соотношения).
Уравнения квантовой механики могут быть формально записаны точно в том же виде, что и уравнения классической механики (гейзенберговское представление в квантовой механике), если заменить физические величины, входящие в уравнения классической механики, соответствующими им Операторы Всё различие между квантовой и классической механикой сведется тогда к различию алгебр. Поэтому Операторы в квантовой механике иногда называют q-числами, в отличие от с-чисел, т. е. обыкновенных чисел, с которыми имеет дело классическая механика.
Операторы можно не только умножать, но и возводить в степень, образовывать из них ряды и рассматривать функции от Операторы Произведение эрмитовых Операторы в общем случае не является эрмитовым. В квантовой механике используются и неэрмитовы Операторы, важным классом которых являются унитарные операторы. Унитарные Операторы не меняют норм («длин») векторов и «углов» между ними. Неизменность нормы вектора состояния даёт возможность интерпретации его компонент как амплитуд вероятности равным образом в исходной и преобразованной функции. Поэтому действием унитарного Операторы описывается развитие квантовомеханической системы во времени, а также её смещение как целого в пространстве, поворот, зеркальное отражение и др. Выполняемые унитарными Операторы преобразования (унитарные преобразования) играют в квантовой механике такую же роль, какую в классической механике играют канонические преобразования (см. Механики уравнения канонические).
В квантовой механике применяется также Операторы комплексного сопряжения, не являющийся линейным. Произведение такого Операторы на унитарный Операторы называются антиунитарным Операторы Антиунитарные Операторы описывают преобразование обращения времени и некоторые др.
В теории квантовых систем, состоящих из тождественных частиц, широко применяется метод квантования вторичного, в котором рассматриваются состояния с неопределённым или переменным числом частиц и вводятся Операторы, действие которых на вектор состояния с данным числом частиц приводит к вектору состояния с измененным на единицу числом частиц (Операторы рождения и поглощения частиц). Операторы рождения или поглощения частицы в данной точке х,  (х) формально подобен волновой функции y(х), как q- и с-числа, отвечающие одной и той же физической величине соответственно в квантовой и классической механике. Такие Операторы образуют квантованные поля, играющие фундаментальную роль в релятивистских квантовых теориях (квантовой электродинамике, теории элементарных частиц; см. Квантовая теория поля).
(х) формально подобен волновой функции y(х), как q- и с-числа, отвечающие одной и той же физической величине соответственно в квантовой и классической механике. Такие Операторы образуют квантованные поля, играющие фундаментальную роль в релятивистских квантовых теориях (квантовой электродинамике, теории элементарных частиц; см. Квантовая теория поля).
Лит. см. при статьях Квантовая механика, Квантовая теория поля.
В. Б. Берестецкий.
| "БСЭ" >> "О" >> "ОП" >> "ОПЕ" |
Статья про "Операторы" в Большой Советской Энциклопедии была прочитана 662 раз
| Коптим скумбрию в коробке |
| Куриный суп |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс