


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Остаточный член
Определение "Остаточный член" в Большой Советской Энциклопедии
Остаточный член приближённой формулы, разность между точным и приближённым значениями представляемого этой формулой выражения. В зависимости от характера приближённой формулы Остаточный член может иметь различный вид. Обычно задача исследования Остаточный член состоит в том, чтобы получить для него оценки. Например, приближённой формуле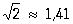
соответствует точное равенство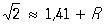 ,
,
где выражение R является Остаточный член для приближения 1,41 к числу 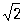 и известно, что 0,004 < R < 0,005. Далее, Остаточный член постоянно встречается в асимптотических формулах. Например, для числа p(х) простых чисел, не превосходящих х, имеем асимптотическую формулу
и известно, что 0,004 < R < 0,005. Далее, Остаточный член постоянно встречается в асимптотических формулах. Например, для числа p(х) простых чисел, не превосходящих х, имеем асимптотическую формулу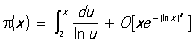 ,
,
где m - любое положительное число, меньшее 3/5; здесь Остаточный член, являющийся разностью
между функциями p(х) и 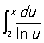 для х ³ 2, записан в виде
для х ³ 2, записан в виде 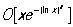 , где буква О обозначает, что Остаточный член не превосходит по абсолютной величине выражения
, где буква О обозначает, что Остаточный член не превосходит по абсолютной величине выражения 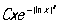 , а С - некоторая положительная постоянная. Можно говорить об Остаточный член формулы, дающей приближённое представление функции. Например, в Тейлора формуле
, а С - некоторая положительная постоянная. Можно говорить об Остаточный член формулы, дающей приближённое представление функции. Например, в Тейлора формуле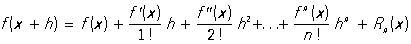
Остаточный член Rn (x) в форме Лагранжа имеет вид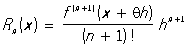 ,
,
где q - некоторое число, причём 0 < q < 1 (q зависит, вообще говоря, от выбранных значений х и h). Наличие в формуле для Rn (x) числа q вносит некоторую неопределённость; такого рода неопределённость свойственна многим формулам для Остаточный член
Можно говорить об Остаточный член квадратурной формулы, интерполяционных формул и т.д.
| "БСЭ" >> "О" >> "ОС" >> "ОСТ" >> "ОСТА" |
Статья про "Остаточный член" в Большой Советской Энциклопедии была прочитана 294 раз
| Бургер двойного помола |
| Буддийская молитва в Камбодже |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс