


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Ошибок теория
Определение "Ошибок теория" в Большой Советской Энциклопедии
Ошибок теория, раздел математической статистики, посвященный построению уточнённых выводов о численных значениях приближённо измеренных величин, а также об ошибках (погрешностях) измерений. Повторные измерения одной и той же постоянной величины дают, как правило, различные результаты, так как каждое измерение содержит некоторую ошибку. Различают 3 основных вида ошибок: систематические, грубые и случайные. Систематические ошибки всё время либо преувеличивают, либо преуменьшают результаты измерений и происходят от определённых причин (неправильной установки измерительных приборов, влияния окружающей среды и т. д.), систематически влияющих на измерения и изменяющих их в одном направлении. Оценка систематических ошибок производится с помощью методов, выходящих за пределы математической статистики (см. Наблюдений обработка). Грубые ошибки возникают в результате просчёта, неправильного чтения показаний измерительного прибора и т. п. Результаты измерений, содержащие грубые ошибки, сильно отличаются от других результатов измерений и поэтому часто бывают хорошо заметны. Случайные ошибки происходят от различных случайных причин, действующих при каждом из отдельных измерений непредвиденным образом то в сторону уменьшения, то в сторону увеличения результатов.
Ошибок теория занимается изучением лишь грубых и случайных ошибок. Основные задачи Ошибок теория: разыскание законов распределения случайных ошибок, разыскание оценок (см. Статистические оценки) неизвестных измеряемых величин по результатам измерений, установление погрешностей таких оценок и устранение грубых ошибок.
Пусть в результате n независимых равноточных измерений некоторой неизвестной величины а получены значения x1, x2,..., xn. Разности
d1 = x1 — a,…, dn = xn — a
называются истинными ошибками. В терминах вероятностной Ошибок теория все di трактуются как случайные величины; независимость измерений понимается как взаимная независимость случайных величин d1,..., dn. Равноточность измерений в широком смысле истолковывается как одинаковая распределённость: истинные ошибки равноточных измерений суть одинаково распределённые случайные величины. При этом математическое ожидание случайных ошибок b = Ed1 =...= Еdn называется систематической ошибкой, а разности d1 — b,..., dn — b — случайными ошибками. Таким образом, отсутствие систематической ошибки означает, что b = 0, и в этой ситуации d1,..., dn суть случайные ошибки. Величину 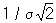 , где а — квадратичное отклонение, называют мерой точности (при наличии систематической ошибки мера точности выражается отношением
, где а — квадратичное отклонение, называют мерой точности (при наличии систематической ошибки мера точности выражается отношением 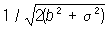 . Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений
. Равноточность измерений в узком смысле понимается как одинаковость меры точности всех результатов измерений. Наличие грубых ошибок означает нарушение равноточности (как в широком, так и в узком смысле) для некоторых отдельных измерений. В качестве оценки неизвестной величины а обычно берут арифметическое среднее из результатов измерений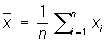 ,
,
а разности D1 = x1 — 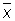 ,..., Dn = xn —
,..., Dn = xn — 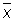 называются кажущимися ошибками. Выбор
называются кажущимися ошибками. Выбор 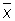 в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка
в качестве оценки для а основан на том, что при достаточно большом числе n равноточных измерений, лишённых систематической ошибки, оценка 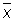 с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон); оценка
с вероятностью, сколь угодно близкой к единице, сколь угодно мало отличается от неизвестной величины а (см. Больших чисел закон); оценка 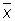 лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
лишена систематической ошибки (оценки с таким свойством называются несмещенными); дисперсия оценки есть
D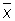 = E (
= E (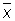 — а)2 = s2/n.
— а)2 = s2/n.
Опыт показывает, что практически очень часто случайные ошибки di подчиняются распределениям, близким к нормальному (причины этого вскрыты так называемыми предельными теоремами теории вероятностей). В этом случае величина 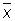 имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s2/n. Если распределения di в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы, не меньше D
имеет мало отличающееся от нормального распределение, с математическим ожиданием а и дисперсией s2/n. Если распределения di в точности нормальны, то дисперсия всякой другой несмещенной оценки для а, например медианы, не меньше D . Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
. Если же распределение di отлично от нормального, то последнее свойство может не иметь места.
Если дисперсия s2 отдельных измерений заранее известна, то для её оценки пользуются величиной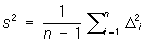
(Es2 = s2, т. е. s2 — несмещенная оценка для s2), если случайные ошибки di имеют нормальное распределение, то отношение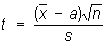
подчиняется Стьюдента распределению с n — 1 степенями свободы. Этим можно воспользоваться для оценки погрешности приближённого равенства а » 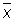 (см. Наименьших квадратов метод).
(см. Наименьших квадратов метод).
Величина (n — 1) s2/s2 при тех же предположениях имеет распределение c2 (см. «Хи-квадрат» распределение) с n — 1 степенями свободы. Это позволяет оценить погрешность приближённого равенства s » s. Можно показать, что относительная погрешность |s — s|Is не будет превышать числа q с вероятностью
w = F (z2, n — 1) — F (z1, n — 1),
где F (z, n — 1) — функция распределения c2,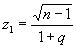 ,
, 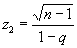 .
.
Лит.: Линник Ю. В., Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962; Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968.
Л. Н. Большев.
| "БСЭ" >> "О" >> "ОШ" |
Статья про "Ошибок теория" в Большой Советской Энциклопедии была прочитана 765 раз
| Коптим скумбрию в коробке |
| Ананасы на гриле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс