


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Параметрическое представление
Определение "Параметрическое представление" в Большой Советской Энциклопедии
Параметрическое представление функции, выражение функциональной зависимости между несколькими переменными посредством вспомогательных переменных параметров. В случае двух переменных х и у зависимость между ними F (х, у) = 0 может быть геометрически истолкована как уравнение некоторой плоской кривой. Любую величину t, определяющую положение точки (х, у) на этой кривой (например, длину дуги, отсчитываемой со знаком + или - от некоторой точки кривой, принятой за начало отсчёта, или момент времени в некотором заданном движении точки, описывающей кривую), можно принять за параметр, в функции которого выразятся х и у:
x = j(t), у = y(t). (*)
Последние функции и дадут Параметрическое представление функциональной зависимости между х и у, уравнения (*) называют параметрическими уравнениями соответствующей кривой. Так, для случая зависимости x2 + y2 = 1 имеем Параметрическое представление х= cos t, у = sin t (0 £ t < 2p) (параметрические уравнения окружности); для случая зависимости х2-у2 = 1 имеем Параметрическое представление 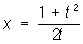 ;
; 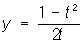 (t ¹ 0) или также х = cosec t, y=ctg t (- p< t < p, t ¹ 0) (параметрические уравнения гиперболы). Если параметр t можно выбрать так, что функции (*) рациональны, то кривую называют уникурсальной (см. Уникурсальная кривая); такой является, например, гипербола. Особенно важно Параметрическое представление пространственных кривых, т. е. задание их уравнениями вида: х = j(t), у = y (t), z = c (t). Так, прямая в пространстве допускает Параметрическое представление х = а + mt; у = b + nt; z = с + pt, винтовая линия - Параметрическое представление х = a cos t; у = a sin t; z = ct.
(t ¹ 0) или также х = cosec t, y=ctg t (- p< t < p, t ¹ 0) (параметрические уравнения гиперболы). Если параметр t можно выбрать так, что функции (*) рациональны, то кривую называют уникурсальной (см. Уникурсальная кривая); такой является, например, гипербола. Особенно важно Параметрическое представление пространственных кривых, т. е. задание их уравнениями вида: х = j(t), у = y (t), z = c (t). Так, прямая в пространстве допускает Параметрическое представление х = а + mt; у = b + nt; z = с + pt, винтовая линия - Параметрическое представление х = a cos t; у = a sin t; z = ct.
Для случая трёх переменных х, у и z, связанных зависимостью F (x, y, z) = 0 (одну из них, например z, можно рассматривать как неявную функцию двух других), геометрическим образом служит поверхность. Чтобы определить положение точки на ней, нужны два параметра u и u (например, широта и долгота на поверхности шара), так что Параметрическое представление имеет вид: х = j(u, u), у = y (u, u); z = c (u, u). Например, для зависимости x2+ y2= (z2+1)2 имеем Параметрическое представление х = (u2-1) cos u; у = (u2 + 1) sinu; z = u. Важнейшими преимуществами Параметрическое представление являются: 1) то, что они дают возможность изучать неявные функции и в тех случаях, когда переход к их явному заданию без посредства параметров затруднителен; 2) то, что здесь удаётся выражать многозначные функции посредством однозначных. Вопросы Параметрическое представление изучены особенно хорошо для аналитических функций. Параметрическое представление аналитических функций посредством однозначных аналитических функций составляет предмет теории униформизации.
| "БСЭ" >> "П" >> "ПА" >> "ПАР" >> "ПАРА" |
Статья про "Параметрическое представление" в Большой Советской Энциклопедии была прочитана 425 раз
| Кукурузный крем суп со скатом |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс