


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Полная система функций
Определение "Полная система функций" в Большой Советской Энциклопедии
Полная система функций, такая система функций Ф = {j(x:)}, определённых на отрезке [a, b], что не существует функции f (x), для которой, 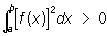 и которая была бы ортогональна ко всем функциям j(х) из Ф, т. е. для которой
и которая была бы ортогональна ко всем функциям j(х) из Ф, т. е. для которой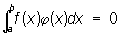
при любой функции j(х) из Ф (интегралы понимаются в смысле Лебега, см. Интеграл). Система функций может быть полной на одном отрезке и не быть полной на другом. Например, 1, sinx, cos х,..., sinnx, cosnx,... образуют Полная система функций на отрезке [0, 2p], но не образуют Полная система функций на отрезке [—2p, 2p]; последнее вытекает из того, что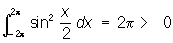
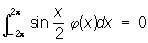
для любой функции j(x) рассматриваемой системы. Для того чтобы система функций с интегрируемым квадратом была Полная система функций, необходимо и достаточно, чтобы любую функцию с интегрируемым квадратом на отрезке [а, b] можно было с любой степенью точности приблизить в среднем линейными комбинациями функций из этой системы. См. Ортогональная система функций.
| "БСЭ" >> "П" >> "ПО" >> "ПОЛ" >> "ПОЛН" |
Статья про "Полная система функций" в Большой Советской Энциклопедии была прочитана 453 раз
| Луковый соус |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс