


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Полунепрерывная функция
Определение "Полунепрерывная функция" в Большой Советской Энциклопедии
Полунепрерывная функция, понятие математического анализа. Полунепрерывная функция снизу (сверху) в точке х0 называется функция, для которой 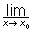 f (x) = f (x0) [соответственно
f (x) = f (x0) [соответственно 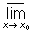 f (x) = f (x0)]. Иначе, функция полунепрерывна снизу в точке x0, если для всякого e > 0 найдётся такое d > 0, что из |x - x0| < d вытекает f (x0) -— f (x) < e (не по абсолютной величине!). Функция, полунепрерывная и снизу и сверху, непрерывна в обычном смысле. Ряд свойств Полунепрерывная функция аналогичен свойствам непрерывных функций (см. Непрерывная функция). Например: 1) если f (x) и g (x) Полунепрерывная функция снизу, то и их сумма и произведение Полунепрерывная функция снизу; 2) Полунепрерывная функция снизу на отрезке достигает своего наименьшего значения. Для рядов Полунепрерывная функция снизу верно, например, следующее утверждение: если un ³ 0 и все un (x) Полунепрерывная функция снизу, то сумма ряда å¥n=1un (x) Полунепрерывная функция снизу. Полунепрерывная функция принадлежат к функциям первого класса по Бэра классификации.
f (x) = f (x0)]. Иначе, функция полунепрерывна снизу в точке x0, если для всякого e > 0 найдётся такое d > 0, что из |x - x0| < d вытекает f (x0) -— f (x) < e (не по абсолютной величине!). Функция, полунепрерывная и снизу и сверху, непрерывна в обычном смысле. Ряд свойств Полунепрерывная функция аналогичен свойствам непрерывных функций (см. Непрерывная функция). Например: 1) если f (x) и g (x) Полунепрерывная функция снизу, то и их сумма и произведение Полунепрерывная функция снизу; 2) Полунепрерывная функция снизу на отрезке достигает своего наименьшего значения. Для рядов Полунепрерывная функция снизу верно, например, следующее утверждение: если un ³ 0 и все un (x) Полунепрерывная функция снизу, то сумма ряда å¥n=1un (x) Полунепрерывная функция снизу. Полунепрерывная функция принадлежат к функциям первого класса по Бэра классификации.
| "БСЭ" >> "П" >> "ПО" >> "ПОЛ" >> "ПОЛУ" |
Статья про "Полунепрерывная функция" в Большой Советской Энциклопедии была прочитана 465 раз
| Коптим скумбрию в коробке |
| Семга на горелке |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс