


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Полуплоскость
Определение "Полуплоскость" в Большой Советской Энциклопедии
Полуплоскость (математическая), совокупность точек плоскости, лежащих по одну сторону от некоторой прямой этой плоскости. Координаты точек Полуплоскость удовлетворяют неравенству Ах + By + С > 0, где А, В, С — некоторые постоянные, причём А и В одновременно не равны нулю. Если сама прямая Ax + By + С = 0 (граница Полуплоскость) причисляется к Полуплоскость, то говорят о замкнутой Полуплоскость
На комплексной плоскости z = х + iy рассматриваются верхняя Полуплоскость у = lmz > 0, нижняя Полуплоскость у = lmz < 0, левая Полуплоскость х = Rez < 0, правая Полуплоскость x = Rez > 0 и т.д. Верхняя Полуплоскость комплексной плоскости z конформно отображается на круг ½w½<1 с помощью дробно-линейной функции 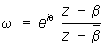 , где q — произвольное действительное число, а Imb > 0.
, где q — произвольное действительное число, а Imb > 0.
| "БСЭ" >> "П" >> "ПО" >> "ПОЛ" >> "ПОЛУ" |
Статья про "Полуплоскость" в Большой Советской Энциклопедии была прочитана 443 раз
| Каша со столетними яйцами |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс