


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Рациональная функция
Определение "Рациональная функция" в Большой Советской Энциклопедии
Рациональная функция, функция, получающаяся в результате конечного числа арифметических операций (сложения, умножения и деления) над переменным х и произвольными числами. Рациональная функция имеет вид: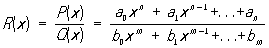 , (1)
, (1)
где a0, a1, ..., an и b0, b1, ..., bm (a0 ¹ 0, b0(0)- постоянные, a n и m - неотрицательные целые числа. Рациональная функция определена и непрерывна для всех значений х, кроме тех, которые являются корнями знаменателя Q (x). Если x - корень кратности k знаменателя Q (x) и одновременно корень кратности r (r ³ k) числителя Р (х), то R (x) имеет в точке x устранимый разрыв; если же r < k, то R (x) имеет в точке x бесконечный разрыв (полюс). Многочлен является частным случаем Рациональная функция (при m = 0), поэтому многочлены иногда называются целыми Рациональная функция; всякая Рациональная функция есть отношение двух многочленов. Др. примером Рациональная функция может служить дробно-линейная функция.
Если в формуле (1) n < m (m > 0), то Рациональная функция называется правильной; если же n ³ m, то R (x) может быть представлена в виде суммы многочлена M (x) степени n - m и правильной Рациональная функция R1(x) = 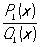 :
:
R (x) = М (х) + R1(x),
многочлены М (х) и P1(x) (степень последнего меньше m) однозначно определяются из соотношения
Р (х) = M (x) Q (x) + P1(x)
(формула деления многочлена с остатком).
Из определения Рациональная функция следует, что функции, получаемые в результате конечного числа арифметических операций над Рациональная функция и произвольными числами, снова являются Рациональная функция В частности, Рациональная функция от Рациональная функция есть вновь Рациональная функция Во всех точках, в которых она определена, Рациональная функция дифференцируема, и её производная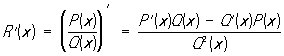
также является Рациональная функция Интеграл от Рациональная функция сводится по предыдущему к сумме интеграла от многочлена и интеграла от правильной Рациональная функция Интеграл от многочлена является многочленом и его вычисление не представляет труда. Для вычисления второго интеграла пользуются формулой разложения правильной Рациональная функция R1(x) на простейшие дроби: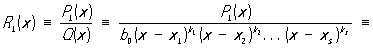
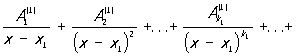
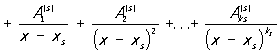
где x1, ..., xs - различные корни многочлена Q (x) соответственно кратностей k1, ..., ks (k1 + ... + ks = m), a 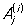 - постоянные коэффициенты. Разложение Рациональная функция на простейшие дроби (2) определяется однозначно. Если коэффициенты многочленов P1(x) и Q (x) - действительные числа, то комплексные корни знаменателя Q (x) (в случае их существования) распадаются на пары сопряжённых, и соответствующие каждой такой паре простейшие дроби в разложении (2) могут быть объединены в вещественные простейшие дроби:
- постоянные коэффициенты. Разложение Рациональная функция на простейшие дроби (2) определяется однозначно. Если коэффициенты многочленов P1(x) и Q (x) - действительные числа, то комплексные корни знаменателя Q (x) (в случае их существования) распадаются на пары сопряжённых, и соответствующие каждой такой паре простейшие дроби в разложении (2) могут быть объединены в вещественные простейшие дроби: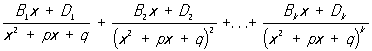
где трёхчлен x2 + px + q имеет комплексно-сопряжённые корни (4q > p2).
Для определения коэффициентов 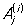 , Bj и Dj можно воспользоваться неопределенных коэффициентов методом. Интегралы от простейших дробей
, Bj и Dj можно воспользоваться неопределенных коэффициентов методом. Интегралы от простейших дробей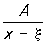 и
и 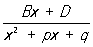
не являются Р. ф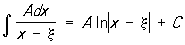 ,
,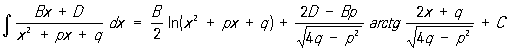
а интегралы от простейших дробей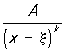 и
и 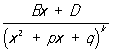
при k > 1 являются: первый - Рациональная функция, а второй - суммой Рациональная функция и интеграла такого же вида, как при k = 1. Т. о., интеграл от любой Рациональная функция (не являющейся многочленом) представляется в виде суммы Рациональная функция, арктангенсов и логарифмических функций. М. В. Остроградский дал алгебраический метод определения рациональной части интеграла от Рациональная функция, не требующий ни разложения Рациональная функция на простейшие дроби, ни интегрирования (см. Остроградского метод).
Рациональная функция являются весьма важным классом элементарных функций. Рассматриваются также Рациональная функция нескольких переменных; они получаются в результате конечного числа арифметических операций над их аргументами и произвольными числами. Так,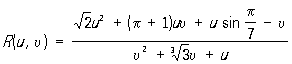
даёт пример Рациональная функция двух переменных u и u.
В середине 20 в. Рациональная функция нашли широкое применение в вопросах приближения функций (см. Приближение и интерполирование функций).
| "БСЭ" >> "Р" >> "РА" >> "РАЦ" |
Статья про "Рациональная функция" в Большой Советской Энциклопедии была прочитана 696 раз
| Бургер двойного помола |
| Сингапурский салат |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс