


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Регулярная точка
Определение "Регулярная точка" в Большой Советской Энциклопедии
Регулярная точка (от лат. regularis - правильный), правильная точка, математический термин, употребляющийся в различных смыслах. Регулярная точка функции f(z) комплексного переменного z = x + iy (i =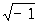 ) - точка z0 = x0 + iy0, в некоторой окрестности ïz - z0ï < r которой функция f(z) однозначна и представима в виде ряда: f(z) =
) - точка z0 = x0 + iy0, в некоторой окрестности ïz - z0ï < r которой функция f(z) однозначна и представима в виде ряда: f(z) = 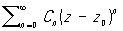 (Cn - постоянные). В аналитической теории дифференциальных уравнений особая точка называется регулярной для уравнения
(Cn - постоянные). В аналитической теории дифференциальных уравнений особая точка называется регулярной для уравнения 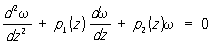 , если она является полюсом порядка не выше k для коэффициентов pk(k = 1, 2). Точка x0 называется Регулярная точка разрыва функции f(x), если f(x0) =
, если она является полюсом порядка не выше k для коэффициентов pk(k = 1, 2). Точка x0 называется Регулярная точка разрыва функции f(x), если f(x0) = 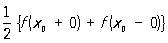 , где f(x0 - 0) и f(x0 + 0) - пределы функции, соответственно, слева и справа. Это понятие находит применение в теории рядов Фурье.
, где f(x0 - 0) и f(x0 + 0) - пределы функции, соответственно, слева и справа. Это понятие находит применение в теории рядов Фурье.
Лит.: Смирнов В. И., Курс высшей математики, 8 изд., т. 3, ч. 2, М., 1969; Маркушевич А. И., Краткий курс теории аналитических функций, 3 изд., М., 1966.
| "БСЭ" >> "Р" >> "РЕ" >> "РЕГ" |
Статья про "Регулярная точка" в Большой Советской Энциклопедии была прочитана 587 раз
| Коптим скумбрию в коробке |
| Яйца в кляре |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс