


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Симплекс
Определение "Симплекс" в Большой Советской Энциклопедии
Симплекс (от лат. simplex - простой) (математический), простейший выпуклый многогранник данного числа измерений n. При n = 3 трёхмерный Симплекс представляет собой произвольный, в том числе неправильный, тетраэдр. Под двумерным Симплекс понимают произвольный треугольник, а под одномерным - отрезок. Нульмерный Симплекс есть просто одна точка.
n-мерный Симплекс имеет n + 1 вершин, не принадлежащих ни к какому (n - 1)-мерному подпространству того евклидова пространства (с числом измерений n или больше), в котором лежит данный Симплекс Обратно, всякие n + 1 точек евклидова n-мерного пространства Rm, m ³ n, не лежащие ни в каком подпространстве менее n измерений, однозначно определяют n-mepный Симплекс с вершинами в заданных точках e0, e1,..., en, он может быть определён как выпуклое замыкание совокупности заданных n + 1 точек, т. е. как пересечение всех выпуклых тел пространства Rm, содержащих эти точки. Если в пространстве Rm дана система декартовых координат x1, х2,..., хт, в которой вершина ei, i = 0, 1,..., n, имеет координаты x1(i), x2(i),..., xm (i), то Симплекс с вершинами e0, e1,..., em состоит из всех точек пространства, координаты которых имеют вид:
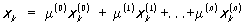 , k = 1,2,..., m, где m(0), m(1),..., m(n) - произвольные неотрицательные числа, дающие в сумме 1. По аналогии со случаем n £ З можно сказать, что все точки Симплекс с данными вершинами получаются, если в эти вершины поместить произвольные неотрицательные массы (из которых по крайней мере одна отлична от нуля) и взять центр тяжести этих масс (дополнительное требование, чтобы сумма всех масс равнялась 1, исключает лишь случай, когда все массы - нулевые).
, k = 1,2,..., m, где m(0), m(1),..., m(n) - произвольные неотрицательные числа, дающие в сумме 1. По аналогии со случаем n £ З можно сказать, что все точки Симплекс с данными вершинами получаются, если в эти вершины поместить произвольные неотрицательные массы (из которых по крайней мере одна отлична от нуля) и взять центр тяжести этих масс (дополнительное требование, чтобы сумма всех масс равнялась 1, исключает лишь случай, когда все массы - нулевые).
Любые r + 1 вершин, 0 £ r £ n - 1, взятые из числа данных n + 1 вершин n-мерного Симплекс, определяют некоторый r-мерный Симплекс - r-мерную грань данного Симплекс Нульмерные грани Симплекс суть его вершины, одномерные грани называются ребрами.
Лит.: Александров П. Симплекс, Комбинаторная топология, М. - Л., 1947; Понтрягин Л. Симплекс, Основы комбинаторной топологии, М. - Л., 1947, с. 23-31.
| "БСЭ" >> "С" >> "СИ" >> "СИМ" >> "СИМП" |
Статья про "Симплекс" в Большой Советской Энциклопедии была прочитана 582 раз
| Бургер двойного помола |
| Кишки на гриле |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс