


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Субгармонические функции
Определение "Субгармонические функции" в Большой Советской Энциклопедии
Субгармонические функции, функции, удовлетворяющие в некоторой области неравенству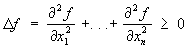 .
.
В случае, когда Df = 0, функция f является гармонической функцией. Понятие Субгармонические функции можно рассматривать как обобщение понятия гармонической функции. При n = 1 условие Df ³ 0 принимает вид 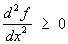 , то есть Субгармонические функции одного переменного есть выпуклая функция. Поэтому понятие Субгармонические функции можно рассматривать также как распространение понятия выпуклой функции на случай любого числа переменных. Так, например, подобно тому как всякая дуга графика выпуклой функции лежит ниже хорды, соединяющей её концы, всякая ограниченная некоторым контуром часть поверхности z = f (x, y), где f (x, у) - Субгармонические функции двух переменных, лежит ниже проходящей через тот же контур поверхности z = F (x, у), где F (x, у) - гармоническая функция (отсюда название «субгармоническая», то есть «подгармоническая»).
, то есть Субгармонические функции одного переменного есть выпуклая функция. Поэтому понятие Субгармонические функции можно рассматривать также как распространение понятия выпуклой функции на случай любого числа переменных. Так, например, подобно тому как всякая дуга графика выпуклой функции лежит ниже хорды, соединяющей её концы, всякая ограниченная некоторым контуром часть поверхности z = f (x, y), где f (x, у) - Субгармонические функции двух переменных, лежит ниже проходящей через тот же контур поверхности z = F (x, у), где F (x, у) - гармоническая функция (отсюда название «субгармоническая», то есть «подгармоническая»).
Приведённое выше определение предполагает, что функция f имеет частные производные второго порядка. От этого ограничения освобождаются, непосредственно выражая отмеченное только что свойство графика Субгармонические функции располагаться ниже графика гармонической функции.
Супергармонические функции (от лат. super - над) - функции, удовлетворяющие неравенству Df £ 0. Если f - супергармоническая функция, то f есть Субгармонические функции, и наоборот. Классические примеры Субгармонические функции и супергармонических функций: для n = 2 логарифмический потенциал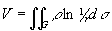
и для n = 3 объёмный потенциал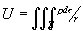
(здесь r - плотность масс или зарядов). Функции эти внутри областей G и Т удовлетворяют соответственно уравнениям Пуассона DV = - 2pr и DU = - 4pr и, следовательно, являются супергармоническими при r ³ 0 и Субгармонические функции при r < 0.
Субгармонические функции применяются, например, при решении задач математической физики (в частности, в теории потенциала), теории случайных процессов.
Лит.: Привалов И. И., Субгармонические функции, М.-Л., 1937.
| "БСЭ" >> "С" >> "СУ" >> "СУБ" |
Статья про "Субгармонические функции" в Большой Советской Энциклопедии была прочитана 512 раз
| Коптим скумбрию в коробке |
| Жаренный морской черенок |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс