


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Френе формулы
Определение "Френе формулы" в Большой Советской Энциклопедии
Френе формулы, формулы, дающие разложение производных (по дуге) единичных векторов касательной t, нормали n и бинормали b произвольной кривой L по векторам t, n, b. Если k и s — кривизна и кручение L, то Френе формулы имеют вид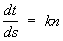 ,
, 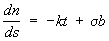 ,
, 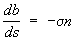 .
.
С помощью Френе формулы исследуются дифференциально-геометрические свойства кривых линий, в кинематике — движение материальной точки по криволинейной траектории.
Френе формулы опубликованы в 1852 французским математиком Ф. Френе (F. Frenet), но были известны ему ещё в 1847; впервые же они были опубликованы в 1851 французским математиком Ж. Серре (J. Serret), почему их иногда называют формулами Серре — Френе.
| "БСЭ" >> "Ф" >> "ФР" >> "ФРЕ" |
Статья про "Френе формулы" в Большой Советской Энциклопедии была прочитана 489 раз
| Бургер двойного помола |
| Каша со столетними яйцами |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс