


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Численное решение уравнений
Определение "Численное решение уравнений" в Большой Советской Энциклопедии
Численное решение уравнений, нахождение приближённых решений алгебраических и трансцендентных уравнений. Численное решение уравнений сводится к выполнению арифметических операций над коэффициентами уравнений и значениями входящих в него функций и позволяет найти решения уравнений с любой наперёд заданной точностью. К Численное решение уравнений сводятся многие задачи математики и её приложений. Хотя общие методы Численное решение уравнений появились лишь в 17 в. (И. Ньютон), но ещё Леонардо Пизанский (начало 13 в.) вычислил корень уравнения х3 + 2x2 + 10x = 20 с ошибкой, меньшей чем 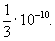 В конце 16 в. И. Бюрги (Швейцария) вычислил корень уравнения 9 — 30x2 + 27x4 — 9x6 + x8 = 0, определяющего длину стороны правильного девятиугольника. Приблизительно в то же время Ф. Виет дал метод вычисления корней алгебраических уравнений, сходный с Ньютона методом.
В конце 16 в. И. Бюрги (Швейцария) вычислил корень уравнения 9 — 30x2 + 27x4 — 9x6 + x8 = 0, определяющего длину стороны правильного девятиугольника. Приблизительно в то же время Ф. Виет дал метод вычисления корней алгебраических уравнений, сходный с Ньютона методом.
Численное решение алгебраических уравнений разбивается на следующие этапы: 1) выделение кратных корней, сводящее задачу к решению уравнения с простыми корнями; 2) определение границ, между которыми могут лежать корни уравнения; 3) разделение корней, т. е. указание промежутков, каждый из которых содержит не более одного простого корня (см. Штурма правило); 4) грубое определение приближённого значения корня, выполняемое графически или каким-либо иным способом (например, при помощи изучения перемен знака левой части уравнения); 5) вычисление корня с заданной точностью. Наиболее распространёнными методами для этого являются методы ложного положения, метод Ньютона, Лобачевского метод, последовательных приближений метод, разложение в ряды и т.д.
При численном решении трансцендентных уравнений ограничиваются этапами 4 и 5. О численном решении дифференциальных уравнений см. в ст. Приближённое решение дифференциальных уравнений.
Лит.: Энциклопедия элементарной математики, кн. 2 — Алгебра, М.—Л., 1951; Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975.
| "БСЭ" >> "Ч" >> "ЧИ" >> "ЧИС" |
Статья про "Численное решение уравнений" в Большой Советской Энциклопедии была прочитана 470 раз
| Коптим скумбрию в коробке |
| Сингапурский салат |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс