


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Элементарные делители
Определение "Элементарные делители" в Большой Советской Энциклопедии
Элементарные делители квадратной матрицы А = ||aiK||1n, степени двучленов
(l - l1) p1, (l - l2) p2,..., (l - ls) ps,
которые получаются из характеристического уравнения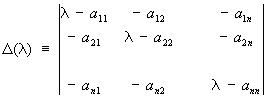
следующим образом. Миноры k-го порядка определителя D(l) (для k £ п) представляют собой многочлены относительно l. Пусть Dk (l) (k = 1, 2,..., n) - наибольший общий делитель всех этих многочленов, Dn (l) = D(l). В ряду каждый многочлен делится на предыдущий без остатка. Если разложить соответствующие частные на линейные множители в поле комплексных чисел: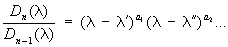
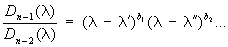
.............................……………………………..,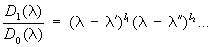
то степени 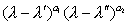 ,...,
,..., 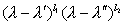 ,... и образуют полную систему Элементарные делители матрицы А (при этом степени с нулевыми показателями не принимаются во внимание). Произведение всех Элементарные делители равно характеристическому многочлену. Элементарные делители определяют нормальную (жорданову) форму матрицы А.
,... и образуют полную систему Элементарные делители матрицы А (при этом степени с нулевыми показателями не принимаются во внимание). Произведение всех Элементарные делители равно характеристическому многочлену. Элементарные делители определяют нормальную (жорданову) форму матрицы А.
| "БСЭ" >> "Э" >> "ЭЛ" >> "ЭЛЕ" >> "ЭЛЕМ" |
Статья про "Элементарные делители" в Большой Советской Энциклопедии была прочитана 521 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Японское море
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Ямполь (пос. гор. типа в Донецкой обл.)
- Балкано-кавказская раса
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс