


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Эллипс (геометрич.)
Определение "Эллипс (геометрич.)" в Большой Советской Энциклопедии
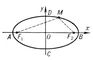 |
| Эллипс. Рис. |
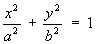 (*)
(*)
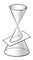 |
| Эллипс. Рис. |
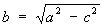 ). Эллипс (геометрич.) — линия второго порядка; она симметрична относительно осей AB и CD; точка О — центр Эллипс (геометрич.) — является его центром симметрии; отрезки AB = 2a и CD = 2b называются соответственно большой и малой осями Эллипс (геометрич.); число е = с/а<1 — эксцентриситет Эллипс (геометрич.) (при е = 0, то есть при а = b, Эллипс (геометрич.) есть окружность). Прямые, уравнения которых x = —а/е и х = а/е, называются директрисами Эллипс (геометрич.); отношение расстояния точки Эллипс (геометрич.) до ближайшего фокуса к расстоянию до ближайшей директрисы постоянно и равно эксцентриситету. Точки А, В, С, D пересечения Эллипс (геометрич.) с осями Ox и Оу называются его вершинами. См. также Конические сечения.
). Эллипс (геометрич.) — линия второго порядка; она симметрична относительно осей AB и CD; точка О — центр Эллипс (геометрич.) — является его центром симметрии; отрезки AB = 2a и CD = 2b называются соответственно большой и малой осями Эллипс (геометрич.); число е = с/а<1 — эксцентриситет Эллипс (геометрич.) (при е = 0, то есть при а = b, Эллипс (геометрич.) есть окружность). Прямые, уравнения которых x = —а/е и х = а/е, называются директрисами Эллипс (геометрич.); отношение расстояния точки Эллипс (геометрич.) до ближайшего фокуса к расстоянию до ближайшей директрисы постоянно и равно эксцентриситету. Точки А, В, С, D пересечения Эллипс (геометрич.) с осями Ox и Оу называются его вершинами. См. также Конические сечения.| "БСЭ" >> "Э" >> "ЭЛ" >> "ЭЛЛ" |
Статья про "Эллипс (геометрич.)" в Большой Советской Энциклопедии была прочитана 627 раз
| Коптим скумбрию в коробке |
| Панайпай |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс