


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Комбинаторика
Определение "Комбинаторика" в Большой Советской Энциклопедии
Комбинаторика, 1) то же, что математический комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов (безразлично, какой природы; это могут быть буквы, цифры, какие-либо предметы и т.п.).
Наиболее употребительные формулы Комбинаторика:
Число размещений. Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (учитывая порядок, в котором выбираются предметы)? Число способов равно
Anm = 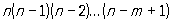
Anm называют числом размещений из n элементов по m.
Число перестановок. Рассмотрим задачу: сколькими способами можно установить порядок следования друг за другом n различных предметов? Число способов равно
Pn = 1Ч2Ч 3... n= n!
(знак n! читается: «n факториал»; оказывается удобным рассматривать также 0!, полагая его равным 1). Pn называют числом перестановок n элементов.
Число сочетаний. Пусть имеется n различных предметов. Сколькими способами можно выбрать из них т предметов (безразлично, в каком порядке выбираются предметы)? Число способов такого выбора равно
Cnm = 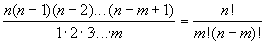
Cnm называют числом сочетаний из n элементов по m. Числа Cnm получаются как коэффициенты разложения n-й степени двучлена (бинома, см. Ньютона бином):
(a+b) n=Cn0 an + Cn1 an-1b +Cn2an-2b2 +... + Cnn-1abn-1 + Cnn bn,
и поэтому они называются также биномиальными коэффициентами. Основные соотношения для биномиальных коэффициентов:
Cnm=Cnn-m, Cnm + Cnm+1 = Cn+1m+1
Cn0 + Cn1 + Cn2 +...+ Cnn-1 + Cnn =2n,
Cn0 — Cn1 + Cn2 —...+ (—1) nCnn = 0.
Числа Anm, Pm и Cnm связаны соотношением:
Anm=Pm Cnm.
Рассматриваются также размещения с повторением (т. е. всевозможные наборы из m предметов n различных видов, порядок в наборе существен) и сочетания с повторением (то же, но порядок в наборе не существен). Число размещений с повторением даётся формулой nm, число сочетаний с повторением — формулой Cmn+m-1.
Основные правила при решении задач Комбинаторика: Правило суммы. Пусть некоторый предмет А может быть выбран из совокупности предметов m способами, а другой предмет В можно выбрать n способами. Тогда имеется т + n возможностей выбрать либо предмет A, либо предмет В.
Правило произведения. Пусть предмет А можно выбрать m способами и после каждого такого выбора предмет В можно выбрать n способами; тогда выбор пары (А, В) в указанном порядке можно осуществить m + n способами.
Принцип включения и исключения. Пусть имеется N предметов, которые могут обладать n свойствами a1, a2,..., an. Обозначим через N (ai, aj,..., ak) число предметов, обладающих свойствами ai, aj,..., ak и, быть может, какими-либо другими свойствами. Тогда число N" предметов, не обладающих ни одним из свойств, a1, a2,..., an, даётся формулой
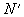 = N—N (a1) — N (a2) —... —N (an) + N (a1, a2) + N (a1, a3) +... + N (an-1, an) — N (a1, a2, a3) —... — N (an-2, an-1, an) +... +(—1) n N (a1,..., an)
= N—N (a1) — N (a2) —... —N (an) + N (a1, a2) + N (a1, a3) +... + N (an-1, an) — N (a1, a2, a3) —... — N (an-2, an-1, an) +... +(—1) n N (a1,..., an)
Лит.: Netto E. Lehrbuch der Combinatorik, 2 Aufl., Lpz. — B., 1927.
В. Е. Тараканов.
| "БСЭ" >> "К" >> "КО" >> "КОМ" >> "КОМБ" |
Статья про "Комбинаторика" в Большой Советской Энциклопедии была прочитана 523 раз
| Салат с Кальмарами |
| Салат с Кальмарами |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс