


БНБ
"БСЭ" (95279)
- Photogallery
- Естественные науки - Математика - Технология
- Авиация и машиностроение
- Высокие технологии
- Вычислительная техника
- Нанотехнология
- Роботехника
- Энергетика
- Электроника
Спирали
Определение "Спирали" в Большой Советской Энциклопедии
 |
| Архимедова спираль |
Уравнение r = аекj задаёт логарифмическую Спирали (см. рис.). Логарифмическая Спирали пересекает под одним и тем же углом а все радиус-векторы, проведённые из полюса, причём ctga = k. Это свойство логарифмической Спирали используется при проектировании вращающихся ножей, фрез и т. д. для достижения постоянства угла резания. Логарифмическая Спирали встречается также в теории спиральных приводов к гидравлическим турбинам и т. д. В теории зубчатых колёс используется возможность качения без скольжения одной логарифмической Спирали по другой, равной с ней, когда обе Спирали вращаются вокруг своих полюсов. При этом получаются зубчатые передачи с переменным передаточным числом. При стереографической проекции плоскости на сферу логарифмической Спирали переходит в локсодромию (кривую, пересекающую все меридианы под одним и тем же углом). Определение длин дуг логарифмической Спирали дано итал. учёным Э. Торричелли. Длина дуги логарифмической Спирали пропорциональна разности длин радиус-векторов, проведённых в концы дуги, точнее равна 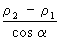 . Швейц. учёный Я. Бернулли показал, что эволюта и каустика (см. Каустическая поверхность) логарифмической Спирали являются логарифмическими Спирали При вращении вокруг полюса логарифмической Спирали получается кривая, гомотетичная (см. Гомотетия) исходной. При инверсии логарифмическая Спирали переходит в логарифмическую Спирали
. Швейц. учёный Я. Бернулли показал, что эволюта и каустика (см. Каустическая поверхность) логарифмической Спирали являются логарифмическими Спирали При вращении вокруг полюса логарифмической Спирали получается кривая, гомотетичная (см. Гомотетия) исходной. При инверсии логарифмическая Спирали переходит в логарифмическую Спирали
Из других Спирали практическое значение имеет Корню Спирали (или клотоида), применяемая при графическом решении некоторых задач дифракции (см. рис.). Параметрическое уравнение этой Спирали имеет вид:
, 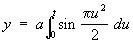 .
.
Корню Спирали является идеальной переходной кривой для закругления железнодорожного пути, так как её радиус кривизны возрастает пропорционально длине дуги. Спирали являются также эвольвенты замкнутых кривых, например эвольвента окружности.
Названия некоторым Спирали даны по сходству их полярных уравнений с уравнениями кривых в декартовых координатах, например параболическая Спирали (см. рис.): (а - r)2 = bj, гиперболическая Спирали(см. рис.): r = а/j. К Спирали относятся также жезл (см. рис.): r2 = a/j и si-ci-cпираль, параметрические уравнения которой имеют вид: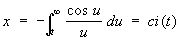 ,
,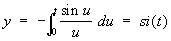
[si (t) и ci (t) - интегральный синус и интегральный косинус]. Кривизна si-ci-cпирали изменяется с длиной дуги по закону показательной функции. Такие Спирали применяют в качестве профиля для лекал.
Напоминает Спирали кривая 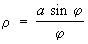 , называемая кохлеоидой (см. рис.). Она бесконечное множество раз проходит через полюс, причём каждый следующий завиток лежит в предыдущем.
, называемая кохлеоидой (см. рис.). Она бесконечное множество раз проходит через полюс, причём каждый следующий завиток лежит в предыдущем.
Спирали встречаются также при рассмотрении особых точек в теории дифференциальных уравнений (см. Особые точки).
Спирали иногда называют также пространственные кривые, делающие бесконечно много оборотов вокруг некоторой оси, например винтовая линия.
Лит. см. при ст. Линия.
| "БСЭ" >> "С" >> "СП" >> "СПИ" |
Статья про "Спирали" в Большой Советской Энциклопедии была прочитана 687 раз
| Бургер двойного помола |
| Луковый соус |
TOP 20
- Лемке Михаил Константинович
- Сульфгидрильные группы
- «Казарменный коммунизм»
- Глициния
- Японское море
- Периодическая система элементов
- Башкирская Автономная Советская Социалистическая Республика
- Иммунитет (историч.)
- Андаманское море
- Сенсуализм
- «Сообразительный»
- Звёздная астрономия
- Балкано-кавказская раса
- Ямполь (пос. гор. типа в Донецкой обл.)
- Навигация (морск.)
- Кульчицкая Елена Львовна
- Мандельштама - Бриллюэна рассеяние
- Театральные учебные заведения
- Электрическая постоянная
- Энсор Джеймс